Doblar papel 42 veces y llegar a la Luna

Si pudiéramos doblar un papel bond de 0,08 milímetros de grosor 42 veces por la mitad, obtendríamos 4.398.046.511.104 capas de papel que, multiplicado por el grosor nos da 351.000 kilómetros, casi la distancia del centro de la Tierra a la Luna.

Si coges un papel y lo doblas por la mitad y lo sigues doblando una y otra vez verás qué pronto resulta imposible seguir haciéndolo. Lo más probable es que no lo puedas doblar más de seis veces, sin que importe mucho el tamaño de la hoja que utilices. Si empleas un papel fino, podrás doblarlo siete veces y con dificultad hasta ocho, pero por muy delgado que sea seguramente no podrás pasar de ahí. En realidad sí que se puede. El récord del mundo consiste en doblar una gran hoja de papel doce veces sobre sí misma. Britney Gallivan consiguió superar el problema llegando nada más y nada menos que a doce dobleces, como se explica en Folding Paper in Half 12 Times. El reto se convirtió en un proyecto de Ciencia de la escuela. Britney elaboró un modelo matemático de lo que sucede al doblar un papel y de cuáles serían las condiciones necesarias para poder hacerlo un gran número de veces, y de ese modo se pudo completar la tarea.



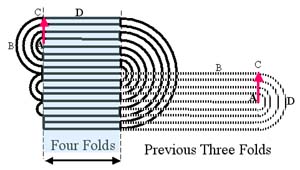
Curiosamente, si pudiéramos seguir doblándolo, rápidamente se produciría un fenómeno aún más sorprendente, ya que el grosor se haría gigantesco. Con un papel normal, cuyo espesor viene a ser de unas 0,8 décimas de milímetro, al doblarlo 42 veces adquiriría un grosor de ¡351.000 kilómetros!, casi la distancia de la Tierra a la Luna.

La base del problema es que el grosor del papel, y el número de «capas», crece de forma exponencial a medida que se va doblando por la mitad, según la fórmula 2ⁿ : 1, 2, 4, 8… 32, 64, 128…

Si doblamos 42 veces, tendremos 24² = 4.398.046.511.104 capas porque cada doblez duplica el número de capas. 0,8 décimas de milímetro del folio x 4.398.046.511.104 capas = 351.843,72 kilómetros. La distancia del papel será de 351.000 kilómetros, casi la distancia de la Tierra a la Luna.